
TP 1 - Mandelbrot
May 2021
You must generate an image corresponding to the mandelbrot fractal as fast as possible. The Mandelbrot set is the set of values of c in the complex plane for which the orbit is 0 under iteration of the quadratic map.
\[z_{n+1} = z_n^2 + c\]
This is done in 3 steps: 1. We compute the image K(x,y), where for for each pixel (x,y) we store the number of iterations until divergence. 2. We compute the histogram of the image K (it will be used for color rendering) 3. We render a color for each (x, y) based on a the histogram normalization of K(x,y) and a colormap.
To opitimize this process, we will use 3 kinds of optimization (in this order): 1. Thread parallelism (TLP) using TBB 2. Algorithmic optimization 3. SIMD (Data level parallelism)
Note that we should normally do (2) before (1), but as we want to practice TLP, we will do it first.
The Mandelbrot set is the set of values of c in the complex plane for which the orbit of 0 under iteration of the quadratic map
\[z_{n+1} = z_n^2 + c\]
is bounded. The image is generated by assigning for each pixel the number k < N such that:
\[ k = \min \{ n \mid |z_n| > 2, n < N \} \]
If there is no such k, we set k = N. The reference uses N = 100.
The pseudo code is given here:
N = 100
For each pixel (px, py) on the output image *count*, do:
{
mx0 = scaled px coordinate of pixel (scaled to lie in the Mandelbrot X scale (-2.5, 1))
my0 = scaled py coordinate of pixel (scaled to lie in the Mandelbrot Y scale (-1, 1))
mx = 0.0
my = 0.0
iteration = 0
while (mx*mx + my*my < 2*2 AND iteration < N) {
mxtemp = mx*mx - my*my + mx0
my = 2*mx*my + my0
mx = mxtemp
iteration = iteration + 1
}
K[px, py] = iteration
}Below is the iteration count per pixel. Black pixels are those for which the iteration count is N. Otherwise they are in gray level from dark (k=0) to white (k=N-1).

Computing the histogram of the image consists in counting the number of occurrence of each value.
Input: Image K
Output: Histogram (array) of size N
histo[x] = 0 for all x;
For each pixel (x,y)
{
k = K(x,y)
histo[k] += 1
}The escape time algorithm is coupled with the histogram coloring algorithm.
For each value k = K(x,y), we normalize this value by the histogram, i.e.:
\[ \begin{align*} \mathrm{total} &= \sum_{i=0}^{N-1} histo[i]\\ \alpha(k) &= \frac{\sum_{i=0}^{k} histo[i]}{\mathrm{total}} \end{align*} \]
The heat color transfer function \(H(\alpha) : (0,1) \rightarrow RGB\) is defined as:
\[ H(x) = \begin{cases} (0, 0, 1) & if & x < 0 \\ (0, \frac{x}{0.25}, 1) & if & x < 0.25 \\ (0, 1, \frac{0.5 - x}{0.25}) & if & 0.25 \le x < 0.5 \\ (\frac{x - 0.5}{0.25}, 1, 0) & if & 0.5 \le x < 0.75 \\ (1, \frac{1 - x}{0.25}, 0) & if & 0.75 \le x < 1 \\ (0, 0, 0) & if & x = 1 \\ \end{cases} \]
So for each pixel (x,y) the final output color is computed as:
output[x,y] = H(α(K[x,y]))
Retrieve the archive a1-login.tar.gz, when building you get to executable:
--help for usage)--help for usage)./view 720 # Generate and diplay on screen in 720p
./view 1080 -o out.bmp # Generate and save to out.bmp in 1080pOnce implemented it should display the following image:
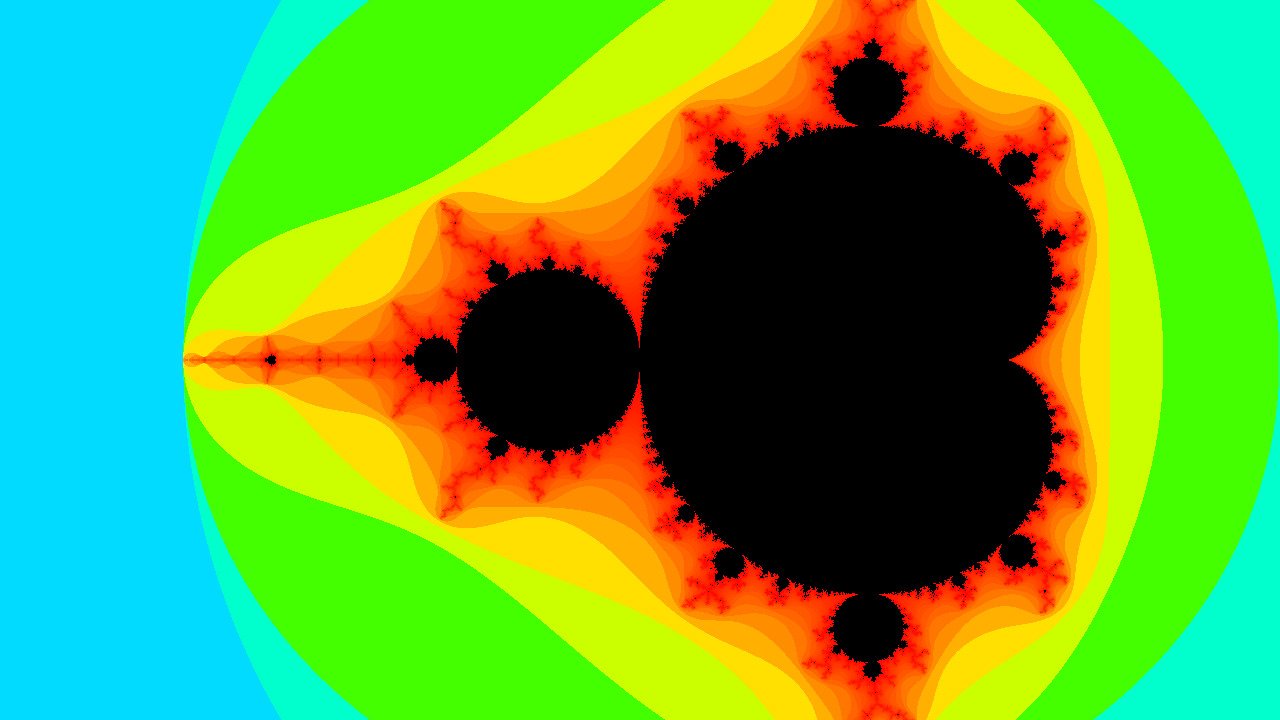
The program bench allows to bench your implementation. It outputs the number of pixels generated by second.
--------------------------------------------------------------------
Benchmark Time CPU Iterations
---------------------------------------------------------------------
BM_Rendering/real_time 210 ms 210 ms 3 9.4044M items/s
BM_Rendering/real_time 210 ms 210 ms 3 9.40018M items/s
BM_Rendering/real_time 210 ms 210 ms 3 9.39969M items/s
BM_Rendering/real_time 210 ms 210 ms 3 9.42455M items/s
BM_Rendering/real_time 210 ms 210 ms 3 9.4181M items/s
BM_Rendering/real_time_mean 210 ms 210 ms 3 9.40938M items/s
BM_Rendering/real_time_median 210 ms 210 ms 3 9.4044M items/s
BM_Rendering/real_time_stddev 0 ms 0 ms 3 11.5549k items/sThe only file you need to edit is src/render.cpp and code the functions:
/// \param buffer The RGB24 image buffer
/// \param width Image width
/// \param height Image height
/// \param stride Number of bytes between two lines
/// \param n_iterations Number of iterations maximal to decide if a point belongs to the mandelbrot set.
void render_base(std::byte* buffer,
int width,
int height,
std::ptrdiff_t stride,
int n_iterations = 100);render_base The serial version of the programrender_mt The multi-threaded version of the programrender_optim The serial version with some algorithmic optimizations.render_simd The serial version with SIMD processingrender_final The version with all optimizations put together!perf to identify bottlenecksUse TBB to perform the processing with multiple threads. Identify the patterns for each of the parts:
Copy/paste the file render.cpp in render_mt.cpp and code the function render_mt. TBB documentation may help here: Parallel for. Bench the new implementaton and measure the speed-up.
The algorithmic optimization should be the first one to implement. Copy/paste the file render.cpp in render_optim.cpp and code the function render_optim. Implement the optimization tricks in order and bench the speed-up.
Symmetry. Because the fractal is symmetric w.r.t the y-axis, only the upper-part of the image needs to be computed and copied to the lower part at the end of the process.
Cardioid / bulb checking enables to knwow if we are in the mandelbrot set and avoids iterating a lot.
Caching the colormap. When assigning colors in the step 3, we can pre-compute a look-up table for each possible k (with know that 0 <= k <= N). Also, computing the cumulated histogram will avoid looping many many times.
\[ \begin{align} CumHisto[k] &= \sum_{i=0}^i histo[i] \\ LUT[k] &= H( \frac{CumHisto[k]}{CumHisto[N]} ) \\ \end{align} \]
and finally, assign Output(x,y) = LUT[ K(x,y) ].
No intermediate buffer / memory. You can use both the output color buffer to store the iteration counter, before storing the color.
union data_t
{
uint16_t iteration_count;
rgb8_t color;
} __attribute__((packed, aligned(1)));and then use: buffer[i].color = LUT[ buffer[i].iteration_count. If you are doing things correctly, you only need to allocate one array of size N for the cumulated histogram.
You will need to use intrinsics and/or clang vector extension: * https://software.intel.com/sites/landingpage/IntrinsicsGuide/ * https://clang.llvm.org/docs/LanguageExtensions.html#vectors-and-extended-vectors
Copy/paste the file render.cpp in render_simd.cpp and code the function render_simd.
The idea is to process 8 consecutives pixels each time. It means, if we are at position (x,y), we will compute the number of iterations for (x,y), (x+1,y), (x+2,y)… (x+7),y.
typedef int int8 __attribute__((ext_vector_type(8)));
typedef float float8 __attribute__((ext_vector_type(8)));
typedef uint16_t ushort8 __attribute__((ext_vector_type(8)));
For each pixel (x, y) with x increments by 8
{
int8 Y = (int8)(y)
int8 X = (int8)(x) + (int8)(0,1,2,3,4,5,6,7)
float8 x0 = scaled x coordinate of pixel (scaled to lie in the Mandelbrot X scale (-2.5, 1))
float8 y0 = scaled y coordinate of pixel (scaled to lie in the Mandelbrot Y scale (-1, 1))
float8 i = (float8)(0.f)
float8 j = (float8)(0.f)
int8 k = (int8)(0)
// 2
for (int i = 0; i < N; ++i)
{
float8 i2 = i*i;
float8 j2 = j*j;
float8 mask = (i2 + j2) < 4.f;
auto test = _mm256_movemask_ps(mask); // Horizontal reduction (all diverged)
if (test) break;
// Update (i,j)
auto xtemp = i2 - j2 + x0;
j = 2.f * i * j + y0;
i = xtemp;
// Update the counter at location of the mask
int8 mask2 = *(reinterpret_cast<int8*>(&mask));
k += (mask2 & int8(0x01));
}
// 3
// Convert and store
ushort8 tmp =__builtin_convertvector(k, ushort8);
_mm_storeu_si128(reinterpret_cast<__m128i*>(&K(x,y)), i);
}The tricky thing here is to use a mask to make conditional operations. Other versions can be found on the internet, i.e. on the Intel AVX extension tutorial, written with pure https://software.intel.com/en-us/articles/introduction-to-intel-advanced-vector-extensions. Feel free to use them as long as you have understood them and are able to explain how they work!
Put all optimizations together. Copy/paste the file render.cpp in render_final.cpp and code the function render_final with DLP, TLP and algorithmics optimizations.