MToS: A Tree of Shapes for Multivariate Images

Authors

Edwin Carlinet, Thierry Géraud

Journal

IEEE Transactions on Image Processing

Type

article

Projects

Olena

Keywords

Image

Date

2015-10-26

Abstract

The Tree of Shapes (ToS) is a morphological tree that provides an high-level hierarchical representation of the image suitable for many image processing tasks. When dealing with color images, one cannot use the ToS because its definition is ill-formed on multivariate data. Common workarounds such as marginal processing, or imposing a total order on data are not satisfactory and yield many problems (color artifacts, loss of invariances...) In this paper, we highlight the need for a self-dual and contrast invariant representation of the image and provide a method that builds a single ToS by merging the shapes computed marginally and preserving the most important properties of the ToS. This method does not try to impose an arbitrary total ordering on values but uses only the inclusion relationship between shapes and the merging strategy works in a shape space. Eventually, we show the relevance of our method and our structure through several applications involving color and multispectral image analysis.

Documents

• Paper

Materials

Multivariate Tree of Shapes Computation Binaries

You can download the x86_64 binaries to compute the Multivariate Tree of Shapes Here. This application outputs 16-bits image where each pixel stores the depth of the node it belongs to. To recover the MToS from this image, one just has to compute its max-tree. Note that the image is twice has big has the original one and has a border for topogical and algorithmic purposes. Thus, any pixel with coordinates (x,y) in the original image is now at coordinates (2*(x+1), 2*(y+1)) in the depth image. The application also outputs a 8bits grayscale version of the depth image that can be used to vizualise the shapes by thresholding this image.

Usage: ./compute_ctos-demo [options] input depth16.tiff depth8.png

• 

  Input RGB Image

• 

  8-bit depth Image

Mumford-Shah Simplification with the MToS

You can download the x86_64 binaries to compute the Mumford-Shah simplification running on the MToS (as described in the paper) Here.

Usage: ./mumford_shah_on_tree_full input[rgb] α₀ α₁ λ output
α₀	Grain filter size before merging trees (0 to disable)
α₁	Grain filter size on the color ToS (0 to disable)
λ	Mumford-shah regularisation weight (e.g. 5000)

• 

  Input RGB Image

• 

  Output Simplified Image

Illustrations

Document detection in videos

In the scope of the ICDAR competition on Smartphone Document Capture and OCR (SmartDoc-2015), we aim at automatically detecting documents in video captured by smartphones. The dataset covers different document layout (textual and/or having graphical content) and realistic scene analysis problems (change of illumination, motion blur, change of perspectives, partial occlusions...).

Grain filters for document layout extraction

We use a grain filter to extract text boxes and graphical parts of documents. Indeed, text parts are composed of letters which are supposed to be small components if the MToS is well-formed. On the contrary, text boxes and grahical contents are large components that should remain after the filtering.

Examples:

• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

More examples are available in this archive.

Interactive object segmentation

We Introduce a method for interactive image segmentation using the MToS. Given a set of markers for the background and foreground classes, we aim at classifying the other pixels to one of these classes. The method performs the classification of the tree nodes and is free of statistical modeling.

• 
• 
• 
• 
• 
• 
• 
• 

Classification of hyperspectral images

We extend the method proposed by Dalla Mura et al. <ref>Dalla Mura, M.; Benediktsson, J.A.; Waske, B.; Bruzzone, L., "Morphological Attribute Profiles for the Analysis of Very High Resolution Images", IEEE Transactions on Geoscience and Remote Sensing, vol.48, no.10, pp.3747,3762, Oct. 2010</ref> using the morphological attribute profiles computed on the MToS to perform the classification of hyperspectral images acquired by Quickbird. We have compared the classification with attributes profiles (AP), the marginal self-dual attribute profiles (MSDAP) and the vectorial self-dual attribute profiles using the MToS(VSDAP). For each method, the same attribute (moment of inertia), the same filtering parameters (0.1, 0.2, . . . , 1.0), and the same classifier (Random Forest) are used.

• 

  Three principal components recomposed as an RGB image.

• 

  Classification ground thruth.

• 

  Classification using attribute profiles. Overall accuracy: 77.5%.

• 

  Classification using marginal self-dual attribute profiles. Overall accuracy: 68.9%.

• 

  Classification using vectorial self-dual attribute profiles (with the MToS). Overall accuracy: 82.2%.

Natural image simplification with the Mumford-Shah functional optimized on the MToS

The method minimizes the Mumford-Shah cartoon model constrained by the tree topology. It removes nodes from the tree until the energy doest not decrease anymore. The tests were performed on the Weizmann database. Some samples are given below and full results are available in this archive.

• Top: original images. Bottom: simplified images.
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

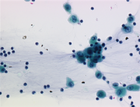
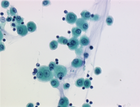
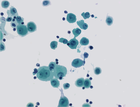
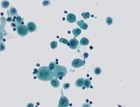
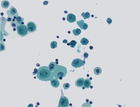
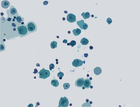
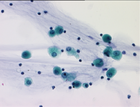
Shapings for bronchial cytology

We aim at simplifying an image by filtering out objects that do not have a given shape in the context of bronchial cytology. We rely on shapings introduced in <ref>Y. Xu, T. Géraud, and L. Najman, "Two applications of shape-based morphology: Blood vessels segmentation and a generalization of constrained connectivity," in Proc. of Intl. Symp. on Mathematical Morphology (ISMM), ser. LNCS, vol. 7883. Springer, 2013, pp. 390–401</ref>. We compute the extinction values of the minima of a two-term energy involving the circularity and the compacity of a shape. We then filter out shapes that are non-minima or minima whose extinction value is below a given threshold t. The bronchial image database can be downloaded here <ref> C. Meurie, O. Lézoray, C. Charrier, and A. Elmoataz, "Combination of multiple pixel classifiers for microscopic image segmentation," IASTED Intl. J. of Robotics and Automation, vol. 20, no. 2, pp. 63–69, 2005. </ref>

• Shape-based filtering with increasing value of extinction value.
• 

  Original

• 

  t=0.01

• 

  t=0.05

• 

  t=0.1

• 

  t=0.2

• 

  Original

• 

  t=0.01

• 

  t=0.05

• 

  t=0.1

• 

  t=0.2

• 

  Original

• 

  t=0.01

• 

  t=0.05

• 

  t=0.1

• 

  t=0.2

<references />

Bibtex (lrde.bib)

@Article{	  carlinet.15.itip,
  author	= {Edwin Carlinet and Thierry G\'eraud},
  title		= {{MToS}: A Tree of Shapes for Multivariate Images},
  journal	= {IEEE Transactions on Image Processing},
  year		= 2015,
  volume	= {24},
  number	= {12},
  pages		= {5330--5342},
  month		= dec,
  abstract	= {The Tree of Shapes (ToS) is a morphological tree that
		  provides an high-level hierarchical representation of the
		  image suitable for many image processing tasks. When
		  dealing with color images, one cannot use the ToS because
		  its definition is ill-formed on multivariate data. Common
		  workarounds such as marginal processing, or imposing a
		  total order on data are not satisfactory and yield many
		  problems (color artifacts, loss of invariances...) In this
		  paper, we highlight the need for a self-dual and contrast
		  invariant representation of the image and provide a method
		  that builds a single ToS by merging the shapes computed
		  marginally and preserving the most important properties of
		  the ToS. This method does not try to impose an arbitrary
		  total ordering on values but uses only the inclusion
		  relationship between shapes and the merging strategy works
		  in a shape space. Eventually, we show the relevance of our
		  method and our structure through several applications
		  involving color and multispectral image analysis.},
  doi		= {10.1109/TIP.2015.2480599}
}