Main Page | Namespace List | Class Hierarchy | Alphabetical List | Class List | File List | Namespace Members | Class Members | File Members | Related Pages | Search for 

oln Namespace Reference

oln namespace. More...


Classes

struct  dpoint_traits< abstract::dpoint< Exact > >
struct  image_traits< abstract::image< Exact > >
struct  image_size_traits< abstract::image_size< Exact > >
struct  image_traits< abstract::image_with_dim< 1, Exact > >
struct  image_traits< abstract::image_with_dim< 2, Exact > >
struct  image_traits< abstract::image_with_dim< 3, Exact > >
struct  image_traits< abstract::image_with_impl< Impl, Exact > >
struct  image_traits< abstract::image_with_type< T, Exact > >
struct  iter_traits< abstract::iter< Exact > >
 Traits for abstract::iter. More...

struct  iter_traits< abstract::iter1d< Exact > >
 Traits for iter::iter1d. More...

struct  iter_traits< abstract::iter2d< Exact > >
 Traits for abstract::iter2d. More...

struct  iter_traits< abstract::iter3d< Exact > >
 Traits for abstract::iter3d. More...

struct  struct_elt_traits< abstract::neighborhood< Exact > >
 Traits for abstract::neighborhood. More...

struct  struct_elt_traits< abstract::neighborhoodnd< Exact > >
 Traits for abstract::neighborhoodnd. More...

struct  point_traits< abstract::point< Exact > >
struct  struct_elt_traits< abstract::struct_elt< Exact > >
 Traits for abstract::struct_elt. More...

struct  struct_elt_traits< abstract::w_window< Exact > >
 Traits for abstract::w_window. More...

struct  struct_elt_traits< abstract::w_windownd< Exact > >
 Traits for abstract::w_windownd. More...

struct  struct_elt_traits< abstract::window< Exact > >
struct  struct_elt_traits< abstract::window_base< Sup, Exact > >
 Traits for abstract::window_base. More...

struct  window_base_friend_traits< abstract::neighborhood< Exact > >
struct  window_base_friend_traits< abstract::window< Exact > >
struct  window_base_friend_traits< abstract::w_window< Exact > >
struct  struct_elt_traits< abstract::windownd< Exact > >
 Traits for abstract::windownd. More...

class  mirror_behavior
class  value_behavior
class  replicate_behavior
 replicate_behavior More...

struct  iter_traits< bkd_iter1d< Exact > >
 Traits for bkd_iter1d. More...

class  bkd_iter1d
 Backward Iterator of 1 dimension. More...

struct  iter_traits< bkd_iter2d< Exact > >
class  bkd_iter2d
struct  iter_traits< bkd_iter3d< Exact > >
class  bkd_iter3d
class  box
struct  f_identity
struct  dpoint_traits< dpoint1d >
class  dpoint1d
struct  dpoint_traits< dpoint2d >
class  dpoint2d
struct  dpoint_traits< dpoint3d >
class  dpoint3d
struct  iter_traits< fwd_iter1d< Exact > >
class  fwd_iter1d
 Forward Iterator on image 1 dimension. More...

struct  iter_traits< fwd_iter2d< Exact > >
class  fwd_iter2d
 Backward Iterator on image 2 dimension. More...

struct  iter_traits< fwd_iter3d< Exact > >
class  fwd_iter3d
 Backward Iterator on image 3 dimension. More...

struct  image_id< image< Dim, T, Impl, Exact > >
struct  image_traits< image< Dim, T, Impl, Exact > >
class  image
struct  mute
struct  dim_traits
struct  image_id< image1d< T, Exact > >
struct  image_traits< image1d< T, Exact > >
class  image1d
struct  image1d::mute
 Define ret equal to image1d<U>. More...

struct  dim_traits< 1, T, Exact >
struct  image_size_traits< image1d_size >
struct  image1d_size
struct  image_id< image2d< T, Exact > >
struct  image_traits< image2d< T, Exact > >
class  image2d
struct  image2d::mute
 Define ret equal to image2d<U>. More...

struct  dim_traits< 2, T, Exact >
struct  image_size_traits< image2d_size >
struct  image2d_size
struct  image_id< image3d< T, Exact > >
struct  image_traits< image3d< T, Exact > >
class  image3d
struct  image3d::mute
 Define ret equal to image3d<U>. More...

struct  dim_traits< 3, T, Exact >
struct  image_size_traits< image3d_size >
struct  image3d_size
struct  impl_traits< impl::image_array< T, Exact > >
struct  impl_traits< impl::image_array1d< T > >
struct  impl_traits< impl::image_array2d< T > >
struct  impl_traits< impl::image_array3d< T > >
struct  impl_traits< impl::image_impl< Exact > >
struct  struct_elt_traits< neighborhood1d >
 Traits for neighborhood1d. More...

class  neighborhood1d
 Neighborhood 1 dimension. More...

struct  struct_elt_traits< neighborhood2d >
 Traits for neighborhood2d. More...

class  neighborhood2d
 Neighborhood 2 dimensions. More...

struct  struct_elt_traits< neighborhood3d >
 Traits for neighborhood3d. More...

class  neighborhood3d
 Neighborhood 3 dimensions. More...

struct  point_traits< point1d >
class  point1d
struct  point_traits< point2d >
class  point2d
struct  point_traits< point3d >
class  point3d
struct  struct_elt_traits< w_window1d< T > >
 Traits for w_windownd1d. More...

class  w_window1d
 Window 1 dimension with weight. More...

struct  struct_elt_traits< w_window2d< T > >
 Traits for w_windownd2d. More...

class  w_window2d
 Window 2 dimensions with weight. More...

struct  struct_elt_traits< w_window3d< T > >
 Traits for w_windownd3d. More...

class  w_window3d
 Window 3 dimensions with weight. More...

struct  struct_elt_traits< window1d >
 Traits for window1d. More...

class  window1d
 Window 1 dimension. More...

struct  struct_elt_traits< window2d >
 Traits for window2d. More...

class  window2d
 Window 2 dimensions. More...

struct  struct_elt_traits< window3d >
 Traits for window3d. More...

class  window3d
 Window 3 dimensions. More...

struct  winiter
struct  winneighb
struct  image_id< morpher::color_morpher< I, Exact > >
 Retrieve types and dimension of the color_morpher. More...

struct  image_traits< morpher::color_morpher< SrcType, Exact > >
 Specialized version for color_morpher. More...

struct  image_traits< morpher::abstract::generic_morpher< SrcType, Exact > >
struct  image_id< morpher::iter_morpher< SrcType, IterType, Exact > >
 Informations about the iter morpher. More...

struct  image_traits< morpher::iter_morpher< SrcType, IterType, Exact > >
 Traits for iter morpher. More...

struct  image_id< morpher::super_piece_morpher< SrcType, Exact > >
 Informations about the super piece morpher. More...

struct  image_id< morpher::piece_morpher< SrcType, Exact > >
 Informations about the piece morpher. More...

struct  image_traits< morpher::piece_morpher< SrcType, Exact > >
 Traits for piece morpher. More...

struct  image_id< morpher::super_slicing_morpher< SrcType, Exact > >
 Informations about the super slicing morpher. More...

struct  image_id< morpher::super_slicing_morpher< const SrcType, Exact > >
 Informations about the const super slicing morpher. More...

struct  image_id< morpher::slicing_morpher< SrcType, Exact > >
 Informations about the slicing morpher. More...

struct  image_id< morpher::slicing_morpher< const SrcType, Exact > >
 Informations about the const slicing morpher. More...

struct  image_traits< morpher::slicing_morpher< SrcType, Exact > >
 Traits for slicing morpher. More...

struct  image_id< oln::morpher::subq_morpher< SrcType, N, Exact > >
struct  image_traits< oln::morpher::subq_morpher< SrcType, N, Exact > >
struct  iter_traits< topo::inter_pixel::bkd_dir_iter< Dim, Exact > >
struct  iter_traits< topo::inter_pixel::fwd_dir_iter< Dim, Exact > >
struct  iter_traits< topo::inter_pixel::internal::dir_iter_< 1, Exact > >
 Traits for iterator for 1D directions. More...

struct  iter_traits< topo::inter_pixel::internal::dir_iter_< 2, Exact > >
 Traits for iterator for 2D directions. More...

struct  iter_traits< topo::inter_pixel::internal::dir_iter_< 3, Exact > >
 Traits for iterator for 3D directions. More...

class  image_traits

Typedefs

typedef int coord
 coord == int


Functions

template<class E> E inter (const abstract::neighborhood< E > &lhs, const abstract::neighborhood< E > &rhs)
 Compute intersection between two neighborhood.

template<class E> E uni (const abstract::neighborhood< E > &lhs, const abstract::neighborhood< E > &rhs)
 Compute union between two neighborhood.

template<class E> struct_elt_traits< E >::win_type mk_win_from_neighb (const abstract::neighborhood< E > &n)
 Construct a window from a neighborhood.

template<class E> E inter (const abstract::w_window< E > &lhs, const abstract::w_window< E > &rhs)
 Compute intersection between two w_windows.

template<class E> E uni (const abstract::w_window< E > &lhs, const abstract::w_window< E > &rhs)
 Compute union between two w_windows.

template<class E> E inter (const abstract::window< E > &lhs, const abstract::window< E > &rhs)
 Compute intersection between two windows.

template<class E> E uni (const abstract::window< E > &lhs, const abstract::window< E > &rhs)
 Compute union between two windows.

template<class AdaptableUnaryFun, class I> mute< I, typename AdaptableUnaryFun::result_type
>::ret 		apply (AdaptableUnaryFun f, const abstract::image< I > &input)
 Standard unary apply procedure. Apply a function f to each element of input.

template<class AdaptableUnaryFun, class I> mute< I, typename AdaptableUnaryFun::result_type
>::ret 		apply (const abstract::image< I > &input)
 Standard unary apply procedure. Apply function f to each element of input, the function is passed as a type and is instantiated. For template functions passed as template-id, one need to instantiate the function for the type of the abstract::image.

template<class AdaptableBinaryFun, class I1, class I2> mute< I1, typename AdaptableBinaryFun::result_type
>::ret 		apply2 (AdaptableBinaryFun f, const abstract::image< I1 > &input1, const abstract::image< I2 > &input2)
 Standard binary apply procedure. Apply function f to each element of input1 and input2.

template<class AdaptableBinaryFun, class I1, class I2> mute< I1, typename AdaptableBinaryFun::result_type
>::ret 		apply2 (const abstract::image< I1 > &input1, const abstract::image< I2 > &input2)
 Standard binary apply procedure. Apply function f to each element of input1 and input2. The function is passed as a type and is instantiated. For template functions passed as template-id, one need to instantiate the function for the type of the abstract::images.

template<template< class > class AdaptableBinaryFun, class I> mute< I, typename AdaptableBinaryFun<
typename mlc::exact< I
>::ret::value_type >::result_type
>::ret 		apply2 (const abstract::image< I > &input1, const abstract::image< I > &input2)
 Standard binary apply procedure. Apply function f to each element of input1 and input2. The function is passed as a type and is instantiated. For template functions passed as template-id, one need to instantiate the function for the type of the abstract::images.

template<class UnaryFun, class I> abstract::image< I > & apply_self (UnaryFun f, abstract::image< I > &input)
 Main apply_self() function. Note only a UnaryFun is required, not a AdaptableUnaryFunc, because as an abstract::image is overwritten, the output type is already known.

template<class UnaryFun, class I> abstract::image< I > & apply_self (abstract::image< I > &input)
 Only a UnaryFun is required, not a AdaptableUnaryFunc, because as an abstract::image is overwritten, the output type is already know. The function is instantiated.

template<class UnaryFun, class I1, class I2> abstract::image< I1 > & apply2_self (UnaryFun f, abstract::image< I1 > &input1, const abstract::image< I2 > &input2)
 Main apply2_exact() function.

template<class UnaryFun, class I1, class I2> abstract::image< I1 > & apply2_self (abstract::image< I1 > &input1, const abstract::image< I1 > &input2)
 The function is instantiated.

template<template< class, class > class UnaryFun, class I1, class I2> abstract::image< I1 > & apply2_self (abstract::image< I1 > &input1, const abstract::image< I2 > &input2)
 If the function is passed as a template-id, it is instantiated for the type of the input elements.

template<template< class > class UnaryFun, class I> abstract::image< I > & apply2_self (abstract::image< I > &input1, const abstract::image< I > &input2)
 If I1 == I2 and the UnaryFun has only one parameter.

mirror_behavior mirror_bhv ()
 To call Ctors with type inference.

template<class T> value_behavior< T > value_bhv (const T &value)
 To call Ctors with type inference.

replicate_behavior replicate_bhv ()
 To call Ctors with type inference.

template<class UF1, class UF2> internal::compose_uu_< UF1,
UF2 > 		compose_uu (const UF1 &f1, const UF2 &f2)
 Compose two unary functors F1 & F2.

template<class UF1, class BF2> internal::compose_ub_< UF1,
BF2 > 		compose_ub (const UF1 &f1, const BF2 &f2)
 Compose a unary functor F1 with a binary functor F2.

template<class BF1, class UF2> internal::compose_bu_< BF1,
UF2 > 		compose_bu (const BF1 &f1, const UF2 &f2)
 Compose a binary functor F1 and an unary functor F2.

template<class AdaptableBinaryFun, class I> AdaptableBinaryFun::result_type fold (AdaptableBinaryFun f, typename mlc::typeadj< typename AdaptableBinaryFun::result_type >::mutable_val val, const abstract::image< I > &input)
 Compute f(...f(f(val,i_0),i_1)...,i_n), where i_0...i_n are the value associated to each abstract::image point. f could return a reference or a const. Make sure VAL is assignable.

template<class AdaptableBinaryFun, class I> AdaptableBinaryFun::result_type fold (AdaptableBinaryFun f, const abstract::image< I > &input)
 Compute f(...f(f(i_0,i_1),i_2)...,i_n), where i_0...i_n are the value associated to each abstract::image point. f could return a reference or a const, so make sure VAL is assignable.

template<class T> void allocate_data_ (T *&buffer, size_t s)
 Allocate an array of s elements of T type.

template<class T> void desallocate_data_ (T *&buffer)
 Free memory pointed to by buffer, then set buffer to 0.

template<class T> void pretreat_1d_data_ (T *&buffer, T *&buffer_, const image1d_size &s)
 Build an image data array with the real data and the border.

template<class T> void pretreat_2d_data_ (T *&buffer, T **&array, const image2d_size &s)
 Build an image data array with the real data and the border.

template<class T> void desallocate_2d_data_ (T **&array, const image2d_size &s)
 Free the image2d data array.

template<class T> void pretreat_3d_data_ (T *&buffer, T **&array2, T ***&array, const image3d_size &s)
 Build an image data array with the real data and the border.

template<class T> void desallocate_3d_data_ (T **&array2, T ***&array, const image3d_size &s)
 Free the image3d data array.

const neighborhood1d & neighb_c2 ()
 Create a neighborhood (1 dimension) with 1 element : 1.

neighborhood1d mk_neighb_segment (unsigned width)
 Create a neighborhood (1 dimension).
  • width The width.


window1d mk_win_from_neighb (const neighborhood1d &n)
 Convert a window (1 dimension) to a neighborhood (1 dimension).
  • n The neighborhood to convert.


const neighborhood2d & neighb_c4 ()
 Create a neighborhood (2 dimension) with 0,1, 1,0.

const neighborhood2d & neighb_c8 ()
 Create a neighborhood (2 dimension) with 4 coordinates: 0,1, 1,1, 1,0, 1,-1.

neighborhood2d mk_neighb_rectangle (unsigned nrows, unsigned ncols)
 Create a rectangular neighborhood (2 dimensions).
  • nrows Number of row.
  • ncols Number of column.


neighborhood2d mk_neighb_square (unsigned width)
 Create a square neighborhood (2 dimensions).
  • width Number of colunm and row.


window2d mk_win_from_neighb (const neighborhood2d &n)
 Convert a window (2 dimensions) to a neighborhood (2 dimensions).
  • n The neighborhood to convert.


const neighborhood3d & neighb_c6 ()
 Create a neighborhood (3 dimension) with 3 coordinates.

const neighborhood3d & neighb_c18 ()
 Create a neighborhood (3 dimension) with 9 coordinates.

const neighborhood3d & neighb_c26 ()
 Create a neighborhood (3 dimension) with 13 coordinates.

neighborhood3d mk_neighb_block (unsigned nslices, unsigned nrows, unsigned ncols)
 Create a block neighborhood (3 dimension).
  • nslices Number of slice.
  • nrows Number of row.
  • ncols Number of column.


neighborhood3d mk_neighb_cube (unsigned width)
 Create a cube neighborhood (3 dimension).
  • width Number of slice, colunm and row.


window3d mk_win_from_neighb (const neighborhood3d &n)
 Convert a window (3 dimensions) to a neighborhood (3 dimensions).
  • n The neighborhood to convert.


template<class I, class F> const F & traverse (F &f, const abstract::image< I > &input)
 Call the functor f on each point of the input image.

template<class F, class I> const F traverse (const abstract::image< I > &input)
 Create a functor f whose type is F<oln_value_type(I), F2<oln_value_type(I)> >, then call it on each point of the input image.

template<class I1, class I2, class F> const F & traverse2 (F &f, const abstract::image< I1 > &input1, const abstract::image< I2 > &input2)
 Call functor f whose type is F on each point of the two input images.

template<template< class > class F, class I> const F< typename mlc::exact<
I >::ret::value_type > 		traverse2 (const abstract::image< I > &input1, const abstract::image< I > &input2)
 Create a functor f whose type is F<oln_value_type(I)>, then call it on each point of the two input images.

template<template< class, class > class F, class I1, class I2> const F< typename mlc::exact<
I1 >::ret::value_type, typename
mlc::exact< I2 >::ret::value_type > 		traverse2 (const abstract::image< I1 > &input1, const abstract::image< I2 > &input2)
 Create a functor f whose type is F<oln_value_type(I1), oln_value_type(I2)>, then call it on each point of the two input images.

template<class T> w_window1d< T > mk_w_win_from_win (T weight, const window1d &win)
 Convert a window (1 dimension) to a w_window (1 dimension).
  • weight The weight to set for each element of the window.
  • win The window to convert.


template<class T> w_window2d< T > mk_w_win_from_win (T weight, const window2d &win)
 Convert a window (2 dimension) to a w_window (2 dimension).
  • weight The weight to set for each element of the window.
  • win The window to convert.


template<class T> w_window3d< T > mk_w_win_from_win (T weight, const window3d &win)
 Convert a window (3 dimension) to a w_window (3 dimension).
  • weight The weight to set for each element of the window.
  • win The window to convert.


const window1d & win_c2_only ()
 Create a window (1 dimension) of 2 elements (-1, 1).

const window1d & win_c2p ()
 Create a window (1 dimension) of 3 elements (-1, 0, 1).

window1d mk_win_segment (unsigned width)
 Create a window (1 dimension) with width elements : -width / 2, ..., 1, 2, ..., width / 2
  • width The width.


const window2d & win_c4_only ()
 Create a window (2 dimensions) of 4 elements.

const window2d & win_c4p ()
 Create a window (2 dimensions) of 5 elements.

const window2d & win_c8_only ()
 Create a window (2 dimensions) of 8 elements.

const window2d & win_c8p ()
 Create a window (2 dimensions) of 9 elements.

window2d mk_win_rectangle (unsigned nrows, unsigned ncols)
 Create a rectangular window (2 dimensions).
  • nrows Number of row.
  • ncols Number of column.


window2d mk_win_ellipse (float yradius, float xradius)
 Create an ellipse window (2 dimensions).

window2d mk_win_square (unsigned width)
 Create a square window (2 dimensions).
  • width Number of column and row.


window2d mk_win_disc (float radius)
 Create a disc window (2 dimensions).
  • radius Radius of the disc.


const window3d & win_c6_only ()
 Create a window (3 dimensions) of 6 elements.

const window3d & win_c6p ()
 Create a window (3 dimensions) of 7 elements.

const window3d & win_c18_only ()
 Create a window (3 dimensions) of 18 elements.

const window3d & win_c18p ()
 Create a window (3 dimensions) of 19 elements.

const window3d & win_c26_only ()
 Create a window (3 dimensions) of 26 elements.

const window3d & win_c26p ()
 Create a window (3 dimensions) of 27 elements.

window3d mk_win_block (unsigned nslices, unsigned nrows, unsigned ncols)
 Create a block window (3 dimension).
  • nslices Number of slice.
  • nrows Number of row.
  • ncols Number of column.


window3d mk_win_ellipsoid (float zradius, float yradius, float xradius)
 Create an ellipsoid window (3 dimension).
  • zradius radius Z.
  • yradius radius Y.
  • xradius radius X.


window3d mk_win_cube (unsigned width)
 Create a cube neighborhood (3 dimension).
  • width Number of slice, colunm and row.


window3d mk_win_ball (float radius)
 Create a ball neighborhood (3 dimension).
  • radius The radius.


Detailed Description

oln namespace.

Function Documentation

template<class T>
void allocate_data_ (  T *&  buffer,
size_t  s
) 
 

Allocate an array of s elements of T type.

Precondition:
s > 0

Definition at line 48 of file image_array.hh.

Referenced by oln::impl::image_array3d< T >::border_reallocate_and_copy_(), oln::impl::image_array2d< T >::border_reallocate_and_copy_(), oln::impl::image_array1d< T >::border_reallocate_and_copy_(), and oln::impl::image_array< T, image_array2d< T > >::image_array(). 

00049   {
00050     precondition(s > 0);
00051     buffer = new T[s];
00052   }

template<class AdaptableUnaryFun, class I>
mute<I, typename AdaptableUnaryFun::result_type>::ret apply (  AdaptableUnaryFun  f,
const abstract::image< I > &  input
)  [inline]
 

Standard unary apply procedure. Apply a function f to each element of input.

Sample of code : Threshold the value of the image.

 #include <oln/basics2d.hh>
 #include <oln/level/threshold.hh>
 #include <ntg/all.hh>
 using namespace ntg;
 int main()
 {
   oln::image2d<int_u8> in = oln::load(IMG_IN "lena256.pgm");
   int_u8 th    = 127;
   rgb_8 low    = rgb_8(100, 0, 0);
   rgb_8 height = rgb_8(0, 200, 255);

   oln::image2d<rgb_8> out
     = apply(oln::level::threshold<int_u8, rgb_8 >(th, low, height),
            in);
   save(out, IMG_OUT "oln_level_threshold.ppm");
 }
lena256_pgm.png
=>
oln_level_threshold.png

Definition at line 75 of file apply.hh.

References oln::abstract::image< Exact >::size().

Referenced by apply(), and oln::level::invert(). 

00076   {
00077     typename mute<I, typename AdaptableUnaryFun::result_type>::ret
00078       output(input.size());
00079     oln_iter_type(I) p(input);
00080     for_all(p) output[p] = f(input[p]);
00081     return output;
00082   }

template<template< class > class AdaptableBinaryFun, class I>
mute<I, typename AdaptableBinaryFun<typename mlc::exact< I >::ret::value_type>::result_type>::ret apply2 (  const abstract::image< I > &  input1,
const abstract::image< I > &  input2
)  [inline]
 

Standard binary apply procedure. Apply function f to each element of input1 and input2. The function is passed as a type and is instantiated. For template functions passed as template-id, one need to instantiate the function for the type of the abstract::images.

Todo:
FIXME: Don't we want to name these functions 'apply()' too?

Definition at line 185 of file apply.hh.

References apply2(). 

00186   {
00187     // Workaround for g++-2.95 bug.
00188     AdaptableBinaryFun<oln_value_type(I)> tmp;
00189     return apply2(tmp, input1, input2);
00190   }

template<class AdaptableBinaryFun, class I1, class I2>
mute< I1, typename AdaptableBinaryFun< typename mlc::exact< I1 >::ret::value_type, typename mlc::exact< I2 >::ret::value_type >::result_type >::ret oln::apply2 (  const abstract::image< I1 > &  input1,
const abstract::image< I2 > &  input2
)  [inline]
 

Standard binary apply procedure. Apply function f to each element of input1 and input2. The function is passed as a type and is instantiated. For template functions passed as template-id, one need to instantiate the function for the type of the abstract::images.

Todo:
FIXME: Don't we want to name these functions 'apply()' too?

Definition at line 148 of file apply.hh.

References apply2(). 

00149   {
00150     return apply2(AdaptableBinaryFun(), input1, input2);
00151   }

template<template< class > class UnaryFun, class I>
abstract::image<I>& apply2_self (  abstract::image< I > &  input1,
const abstract::image< I > &  input2
)  [inline]
 

If I1 == I2 and the UnaryFun has only one parameter.

See also:
apply_self()

Definition at line 283 of file apply.hh.

References apply2_self(). 

00284   {
00285     // Workaround for g++-2.95 bug.
00286     UnaryFun<oln_value_type(I)> tmp;
00287     return apply2_self(tmp, input1, input2);
00288   }

template<template< class, class > class UnaryFun, class I1, class I2>
abstract::image<I1>& apply2_self (  abstract::image< I1 > &  input1,
const abstract::image< I2 > &  input2
)  [inline]
 

If the function is passed as a template-id, it is instantiated for the type of the input elements.

See also:
apply_self()

Definition at line 270 of file apply.hh.

References apply2_self(). 

00271   {
00272     // Workaround for g++-2.95 bug.
00273     UnaryFun<oln_value_type(I1),oln_value_type(I2)> tmp;
00274     return apply2_self(tmp, input1, input2);
00275   }

template<class UnaryFun, class I1, class I2>
abstract::image<I1>& apply2_self (  abstract::image< I1 > &  input1,
const abstract::image< I1 > &  input2
)  [inline]
 

The function is instantiated.

See also:
apply_self()

Definition at line 258 of file apply.hh.

References apply_self(). 

00259   {
00260     return apply_self(UnaryFun(), input1, input2);
00261   }

template<class UnaryFun, class I1, class I2>
abstract::image<I1>& apply2_self (  UnaryFun  f,
abstract::image< I1 > &  input1,
const abstract::image< I2 > &  input2
) 
 

Main apply2_exact() function.

See also:
apply_self()

Definition at line 243 of file apply.hh.

References oln::abstract::image< Exact >::size().

Referenced by apply2_self(). 

00245   {
00246     precondition(input1.size() == input2.size());
00247     oln_iter_type(I1) p(input1);
00248     for_all(p) input1[p] = f(input1[p], input2[p]);
00249     return input1;
00250   }

template<class T>
void desallocate_data_ (  T *&  buffer  ) 
 

Free memory pointed to by buffer, then set buffer to 0.

Precondition:
buffer != 0

Definition at line 61 of file image_array.hh.

Referenced by oln::impl::image_array3d< T >::border_reallocate_and_copy_(), oln::impl::image_array2d< T >::border_reallocate_and_copy_(), and oln::impl::image_array1d< T >::border_reallocate_and_copy_(). 

00062   {
00063     precondition(buffer != 0);
00064     delete[] buffer;
00065     buffer = 0; // security
00066   }

template<class AdaptableBinaryFun, class I>
AdaptableBinaryFun::result_type fold (  AdaptableBinaryFun  f,
const abstract::image< I > &  input
)  [inline]
 

Compute f(...f(f(i_0,i_1),i_2)...,i_n), where i_0...i_n are the value associated to each abstract::image point. f could return a reference or a const, so make sure VAL is assignable.

Todo:
FIXME: Ensure that first_argument_type == result_type.

Definition at line 69 of file fold.hh. 

00070   {
00071     oln_iter_type(I) p(input);
00072     p = begin;
00073     typename mlc::typeadj<
00074       typename AdaptableBinaryFun::result_type>::mutable_val val
00075         = input[p];
00076     for_all_remaining(p)
00077       val = f(val, input[p]);
00078     return val;
00079   }

template<class AdaptableBinaryFun, class I>
AdaptableBinaryFun::result_type fold (  AdaptableBinaryFun  f,
typename mlc::typeadj< typename AdaptableBinaryFun::result_type >::mutable_val  val,
const abstract::image< I > &  input
)  [inline]
 

Compute f(...f(f(val,i_0),i_1)...,i_n), where i_0...i_n are the value associated to each abstract::image point. f could return a reference or a const. Make sure VAL is assignable.

Todo:
FIXME: Ensure that first_argument_type == result_type.

Definition at line 49 of file fold.hh. 

00053   {
00054     oln_iter_type(I) p(input);
00055     for_all(p)
00056       val = f(val, input[p]);
00057     return val;
00058   }

neighborhood3d mk_neighb_block (  unsigned  nslices,
unsigned  nrows,
unsigned  ncols
)  [inline]
 

Create a block neighborhood (3 dimension).

  • nslices Number of slice.
  • nrows Number of row.
  • ncols Number of column.

Returns:
The new neighborhood (3d).
Precondition:
nslices >= 3.

nslices 2 == 1.

nrows >= 3.

nrows 2 == 1.

ncols >= 3.

ncols 2 == 1.

Definition at line 247 of file neighborhood3d.hh.

References oln::neighborhood3d::add(), and coord.

Referenced by mk_neighb_cube(). 

00248   {
00249     precondition(nslices >= 3 && (nslices % 2) == 1);
00250     precondition(nrows >= 3 && (nrows % 2) == 1);
00251     precondition(ncols >= 3 && (ncols % 2) == 1);
00252     neighborhood3d neighb(nrows * ncols);
00253     int half_nslices = nslices / 2;
00254     int half_nrows = nrows / 2;
00255     int half_ncols = ncols / 2;
00256     for (coord slice = - half_nslices; slice <= half_nslices; ++slice)
00257       for (coord row = - half_nrows; row <= half_nrows; ++row)
00258         for (coord col = (slice > 0) ? 0 : 1 ; col <= half_ncols; ++col)
00259             neighb.add(slice, row, col);
00260     return neighb;
00261   }

neighborhood3d mk_neighb_cube (  unsigned  width  )  [inline]
 

Create a cube neighborhood (3 dimension).

  • width Number of slice, colunm and row.

Returns:
The new neighborhood (3d).

Definition at line 269 of file neighborhood3d.hh.

References mk_neighb_block(). 

00270   {
00271     return mk_neighb_block(width, width, width);
00272   }

neighborhood2d mk_neighb_rectangle (  unsigned  nrows,
unsigned  ncols
)  [inline]
 

Create a rectangular neighborhood (2 dimensions).

  • nrows Number of row.
  • ncols Number of column.

Returns:
The new neighborhood (2d).
Precondition:
nrows >= 3.

nrows 2 == 1.

ncols >= 3.

ncols 2 == 1.

Definition at line 218 of file neighborhood2d.hh.

References oln::neighborhood2d::add(), and coord.

Referenced by mk_neighb_square(). 

00219   {
00220     precondition(nrows >= 3 && (nrows % 2) == 1);
00221     precondition(ncols >= 3 && (ncols % 2) == 1);
00222     neighborhood2d neighb(nrows * ncols);
00223     int half_nrows = nrows / 2, half_ncols = ncols / 2;
00224     for (coord row = - half_nrows; row <= half_nrows; ++row)
00225       for (coord col = (row <= 0)? 1 : 0; col <= half_ncols; ++col)
00226           neighb.add(row, col);
00227     return neighb;
00228   }

neighborhood1d mk_neighb_segment (  unsigned  width  )  [inline]
 

Create a neighborhood (1 dimension).

  • width The width.

Returns:
The new neighborhood.
Precondition:
width >= 3.

width 2 == 1.

Add elements of coordinates 1, ..., width / 2.

Definition at line 193 of file neighborhood1d.hh.

References oln::neighborhood1d::add(), and coord. 

00194   {
00195     precondition(width>= 3 && (width % 2) == 1);
00196     neighborhood1d neighb(width);
00197     int half_ncols = width / 2;
00198     for (coord col = 1; col <= half_ncols; ++col)
00199         neighb.add(col);
00200     return neighb;
00201   }

neighborhood2d mk_neighb_square (  unsigned  width  )  [inline]
 

Create a square neighborhood (2 dimensions).

  • width Number of colunm and row.

Returns:
The new neighborhood (2d).

Definition at line 236 of file neighborhood2d.hh.

References mk_neighb_rectangle(). 

00237   {
00238     return mk_neighb_rectangle(width, width);
00239   }

template<class T>
w_window3d<T> mk_w_win_from_win (  T  weight,
const window3d &  win
) 
 

Convert a window (3 dimension) to a w_window (3 dimension).

  • weight The weight to set for each element of the window.
  • win The window to convert.

Returns:
The new w_window.

Definition at line 208 of file w_window3d.hh.

References oln::w_window3d< T >::add(), oln::abstract::struct_elt< window3d >::card(), and oln::abstract::struct_elt< window3d >::dp(). 

00209   {
00210     w_window3d<T> w_win(win.card());
00211     for (unsigned i = 0; i < win.card(); ++i)
00212       w_win.add(win.dp(i), weight);
00213     return w_win;
00214   }

template<class T>
w_window2d<T> mk_w_win_from_win (  T  weight,
const window2d &  win
) 
 

Convert a window (2 dimension) to a w_window (2 dimension).

  • weight The weight to set for each element of the window.
  • win The window to convert.

Returns:
The new w_window.

Definition at line 221 of file w_window2d.hh.

References oln::w_window2d< T >::add(), oln::abstract::struct_elt< window2d >::card(), and oln::abstract::struct_elt< window2d >::dp(). 

00222   {
00223     w_window2d<T> w_win(win.card());
00224     for (unsigned i = 0; i < win.card(); ++i)
00225       w_win.add(win.dp(i), weight);
00226     return w_win;
00227   }

template<class T>
w_window1d<T> mk_w_win_from_win (  T  weight,
const window1d &  win
) 
 

Convert a window (1 dimension) to a w_window (1 dimension).

  • weight The weight to set for each element of the window.
  • win The window to convert.

Returns:
The new w_window.

Definition at line 200 of file w_window1d.hh.

References oln::w_window1d< T >::add(), oln::abstract::struct_elt< window1d >::card(), and oln::abstract::struct_elt< window1d >::dp(). 

00201   {
00202     w_window1d<T> w_win(win.card());
00203     for (unsigned i = 0; i < win.card(); ++i)
00204       w_win.add(win.dp(i), weight);
00205     return w_win;
00206   }

window3d mk_win_ball (  float  radius  )  [inline]
 

Create a ball neighborhood (3 dimension).

  • radius The radius.

Returns:
The new neighborhood (3d).

Definition at line 443 of file window3d.hh.

References mk_win_ellipsoid(). 

00444   {
00445     return mk_win_ellipsoid(radius, radius, radius);
00446   }

window3d mk_win_block (  unsigned  nslices,
unsigned  nrows,
unsigned  ncols
)  [inline]
 

Create a block window (3 dimension).

  • nslices Number of slice.
  • nrows Number of row.
  • ncols Number of column.

Returns:
The new window (3d).
Precondition:
nslices >= 3.

nslices 2 == 1.

nrows >= 3.

nrows 2 == 1.

ncols >= 3.

ncols 2 == 1.

Definition at line 363 of file window3d.hh.

References oln::window3d::add(), and coord.

Referenced by mk_win_cube(). 

00364   {
00365     precondition(nslices >= 3 && (nslices % 2) == 1);
00366     precondition(nrows >= 3 && (nrows % 2) == 1);
00367     precondition(ncols >= 3 && (ncols % 2) == 1);
00368     window3d win(nrows * ncols);
00369     int half_nslices = nslices / 2;
00370     int half_nrows = nrows / 2;
00371     int half_ncols = ncols / 2;
00372     for (coord slice = - half_nslices; slice <= half_nslices; ++slice)
00373       for (coord row = - half_nrows; row <= half_nrows; ++row)
00374         for (coord col = - half_ncols; col <= half_ncols; ++col)
00375           win.add(slice, row, col);
00376     return win;
00377   }

window3d mk_win_cube (  unsigned  width  )  [inline]
 

Create a cube neighborhood (3 dimension).

  • width Number of slice, colunm and row.

Returns:
The new neighborhood (3d).

Definition at line 432 of file window3d.hh.

References mk_win_block(). 

00433   {
00434     return mk_win_block(width, width, width);
00435   }

window2d mk_win_disc (  float  radius  )  [inline]
 

Create a disc window (2 dimensions).

  • radius Radius of the disc.

Returns:
The new window (2d).

Definition at line 308 of file window2d.hh.

References mk_win_ellipse(). 

00309   {
00310     return mk_win_ellipse(radius, radius);
00311   }

window2d mk_win_ellipse (  float  yradius,
float  xradius
)  [inline]
 

Create an ellipse window (2 dimensions).

Returns:
The new window.
The ellipse formula is : $$\frac{x^2}{xradius^2} + \frac{y^2}{yradius^2} = 1$$

Definition at line 266 of file window2d.hh.

References oln::window2d::add(), and coord.

Referenced by mk_win_disc(). 

00267   {
00268     precondition(yradius > 0);
00269     precondition(xradius > 0);
00270 
00271     window2d win;
00272     coord ymax = (coord)roundf(yradius);
00273     float yr2 = yradius * yradius;
00274     for (coord y = -ymax; y <= ymax; ++y)
00275       {
00276         /*
00277               x^2         y^2
00278            --------- + --------- = 1
00279            xradius^2   yradius^2
00280 
00281         */
00282         float v = 1 - y * y / yr2;
00283         if (v < 0) v = 0;       // Can happen because ymax has been rounded.
00284         coord xmax = (coord)roundf(xradius * sqrtf(v));
00285         for (coord x = -xmax; x <= xmax; ++x)
00286           win.add(y, x);
00287       }
00288     return win;
00289   }

window3d mk_win_ellipsoid (  float  zradius,
float  yradius,
float  xradius
)  [inline]
 

Create an ellipsoid window (3 dimension).

  • zradius radius Z.
  • yradius radius Y.
  • xradius radius X.

Precondition:
zradius > 0

yradius > 0

xradius > 0

The ellipsoid formula is : $$\frac{x^2}{xradius^2} + \frac{y^2}{yradius^2} + \frac{z^2}{zradius^2} = 1$$

Definition at line 392 of file window3d.hh.

References oln::window3d::add(), and coord.

Referenced by mk_win_ball(). 

00393   {
00394     precondition(zradius > 0);
00395     precondition(yradius > 0);
00396     precondition(xradius > 0);
00397 
00398     window3d win;
00399     coord zmax = (coord)roundf(zradius);
00400     float zr2 = zradius * zradius;
00401     float yr2 = yradius * yradius;
00402     for (coord z = -zmax; z <= zmax; ++z)
00403       {
00404         /*
00405               x^2         y^2         z^2
00406            --------- + --------- + --------- = 1
00407            xradius^2   yradius^2   zradius^2
00408         */
00409 
00410         /* Set x to 0 in the above formula to find ymax.  */
00411         float v = 1 - z * z / zr2;
00412         if (v < 0) v = 0;       // Can happen because zmax has been rounded.
00413         coord ymax = (coord)roundf(yradius * sqrtf(v));
00414         for (coord y = -ymax; y <= ymax; ++y)
00415           {
00416             float w = v - y * y / yr2;
00417             if (w < 0) w = 0;   // Can happen because ymax has been rounded.
00418             coord xmax = (coord)roundf(xradius * sqrtf(w));
00419             for (coord x = -xmax; x <= xmax; ++x)
00420               win.add(z, y, x);
00421           }
00422       }
00423     return win;
00424   }

window3d mk_win_from_neighb (  const neighborhood3d &  n  )  [inline]
 

Convert a window (3 dimensions) to a neighborhood (3 dimensions).

  • n The neighborhood to convert.

Returns:
The new window.

Definition at line 280 of file neighborhood3d.hh.

References oln::window3d::add(), oln::abstract::neighborhood< neighborhood3d >::card(), and oln::abstract::neighborhood< neighborhood3d >::dp(). 

00281   {
00282     window3d win(n.card());
00283     for (unsigned i = 0; i < n.card(); ++i)
00284       win.add(n.dp(i));
00285     return win;
00286   }

window2d mk_win_from_neighb (  const neighborhood2d &  n  )  [inline]
 

Convert a window (2 dimensions) to a neighborhood (2 dimensions).

  • n The neighborhood to convert.

Returns:
The new window.

Definition at line 247 of file neighborhood2d.hh.

References oln::window2d::add(), oln::abstract::neighborhood< neighborhood2d >::card(), and oln::abstract::neighborhood< neighborhood2d >::dp(). 

00248   {
00249     window2d win(n.card());
00250     for (unsigned i = 0; i < n.card(); ++i)
00251       win.add(n.dp(i));
00252     return win;
00253   }

window1d mk_win_from_neighb (  const neighborhood1d &  n  )  [inline]
 

Convert a window (1 dimension) to a neighborhood (1 dimension).

  • n The neighborhood to convert.

Returns:
The new window.

Definition at line 209 of file neighborhood1d.hh.

References oln::window1d::add(), oln::abstract::neighborhood< neighborhood1d >::card(), and oln::abstract::neighborhood< neighborhood1d >::dp(). 

00210   {
00211     window1d win(n.card());
00212     for (unsigned i = 0; i < n.card(); ++i)
00213       win.add(n.dp(i));
00214     return win;
00215   }

window2d mk_win_rectangle (  unsigned  nrows,
unsigned  ncols
)  [inline]
 

Create a rectangular window (2 dimensions).

  • nrows Number of row.
  • ncols Number of column.

Returns:
The new window (2d).
Precondition:
nrows >= 3.

nrows 2 == 1.

ncols >= 3.

ncols 2 == 1.

Definition at line 246 of file window2d.hh.

References oln::window2d::add(), and coord.

Referenced by mk_win_square(). 

00247   {
00248     precondition(nrows >= 3 && (nrows % 2) == 1);
00249     precondition(ncols >= 3 && (ncols % 2) == 1);
00250     window2d win(nrows * ncols);
00251     int half_nrows = nrows / 2, half_ncols = ncols / 2;
00252     for (coord row = - half_nrows; row <= half_nrows; ++row)
00253       for (coord col = - half_ncols; col <= half_ncols; ++col)
00254         win.add(row, col);
00255     return win;
00256   }

window1d mk_win_segment (  unsigned  width  )  [inline]
 

Create a window (1 dimension) with width elements : -width / 2, ..., 1, 2, ..., width / 2

  • width The width.

Returns:
The new neighborhood.
Precondition:
width >= 3.

width 2 == 1.

Definition at line 203 of file window1d.hh.

References oln::window1d::add(), and coord. 

00204   {
00205     precondition(width>= 3 && (width % 2) == 1);
00206     window1d win(width);
00207     int half_ncols = width / 2;
00208     for (coord col = - half_ncols; col <= half_ncols; ++col)
00209       win.add(col);
00210     return win;
00211   }

window2d mk_win_square (  unsigned  width  )  [inline]
 

Create a square window (2 dimensions).

  • width Number of column and row.

Returns:
The new window (2d).

Definition at line 297 of file window2d.hh.

References mk_win_rectangle(). 

00298   {
00299     return mk_win_rectangle(width, width);
00300   }

const neighborhood3d& neighb_c18 (   )  [inline]
 

Create a neighborhood (3 dimension) with 9 coordinates.

Returns:
The new neighborhood.

Definition at line 192 of file neighborhood3d.hh.

References coord. 

00193   {
00194     static const coord crd[] = { 0,  0,  1,
00195                                  0,  1, -1,
00196                                  0,  1,  0,
00197                                  0,  1,  1,
00198                                  1, -1,  0,
00199                                  1,  0, -1,
00200                                  1,  0,  0,
00201                                  1,  0,  1,
00202                                  1,  1,  0 };
00203     static neighborhood3d neighb(9, crd);
00204     return neighb;
00205   }

const neighborhood1d& neighb_c2 (   )  [inline]
 

Create a neighborhood (1 dimension) with 1 element : 1.

Returns:
The new neighborhood.

Definition at line 176 of file neighborhood1d.hh.

References coord. 

00177   {
00178     static const coord crd[] = {  1 };
00179     static const neighborhood1d neighb(1, crd);
00180     return neighb;
00181   }

const neighborhood3d& neighb_c26 (   )  [inline]
 

Create a neighborhood (3 dimension) with 13 coordinates.

Returns:
The new neighborhood.

Definition at line 212 of file neighborhood3d.hh.

References coord. 

00213   {
00214     static const coord crd[] = { 0,  0,  1,
00215                                  0,  1, -1,
00216                                  0,  1,  0,
00217                                  0,  1,  1,
00218                                  1, -1, -1,
00219                                  1, -1,  0,
00220                                  1, -1,  1,
00221                                  1,  0, -1,
00222                                  1,  0,  0,
00223                                  1,  0,  1,
00224                                  1,  1, -1,
00225                                  1,  1,  0,
00226                                  1,  1,  1 };
00227     static neighborhood3d neighb(13, crd);
00228     return neighb;
00229   }

const neighborhood2d& neighb_c4 (   )  [inline]
 

Create a neighborhood (2 dimension) with 0,1, 1,0.

Returns:
The new neighborhood.

Definition at line 184 of file neighborhood2d.hh.

References coord. 

00185   {
00186     static const coord crd[] = { 0,1,  1,0 };
00187     static const neighborhood2d neighb(2, crd);
00188     return neighb;
00189   }

const neighborhood3d& neighb_c6 (   )  [inline]
 

Create a neighborhood (3 dimension) with 3 coordinates.

Returns:
The new neighborhood.

Definition at line 178 of file neighborhood3d.hh.

References coord. 

00179   {
00180     static const coord crd[] = { 0,  0,  1,
00181                                  0,  1,  0,
00182                                  1,  0,  0};
00183     static const neighborhood3d neighb(3, crd);
00184     return neighb;
00185   }

const neighborhood2d& neighb_c8 (   )  [inline]
 

Create a neighborhood (2 dimension) with 4 coordinates: 0,1, 1,1, 1,0, 1,-1.

Returns:
The new neighborhood.

Definition at line 198 of file neighborhood2d.hh.

References coord. 

00199   {
00200     static const coord crd[] = { 0,1,  1,1,  1,0,  1,-1 };
00201     static const neighborhood2d neighb(4, crd);
00202     return neighb;
00203   }

template<template< class, class > class F, class I1, class I2>
const F<typename mlc::exact< I1 >::ret::value_type, typename mlc::exact< I2 >::ret::value_type> traverse2 (  const abstract::image< I1 > &  input1,
const abstract::image< I2 > &  input2
)  [inline]
 

Create a functor f whose type is F<oln_value_type(I1), oln_value_type(I2)>, then call it on each point of the two input images.

Precondition:
input1.size() == input2.size()

Definition at line 145 of file traverse.hh.

References traverse2(). 

00147   {
00148     F<oln_value_type(I1), oln_value_type(I2)> f;
00149     return traverse2(f, input1, input2);
00150   }

template<template< class > class F, class I>
const F<typename mlc::exact< I >::ret::value_type> traverse2 (  const abstract::image< I > &  input1,
const abstract::image< I > &  input2
)  [inline]
 

Create a functor f whose type is F<oln_value_type(I)>, then call it on each point of the two input images.

Precondition:
input1.size() == input2.size()

Definition at line 130 of file traverse.hh.

References traverse2(). 

00131   {
00132     F<oln_value_type(I)> f;
00133     return traverse2(f, input1, input2);
00134   }

template<class I1, class I2, class F>
const F& traverse2 (  F &  f,
const abstract::image< I1 > &  input1,
const abstract::image< I2 > &  input2
) 
 

Call functor f whose type is F on each point of the two input images.

Precondition:
input1.size() == input2.size()

Definition at line 112 of file traverse.hh.

References oln::abstract::image< Exact >::size().

Referenced by traverse2(). 

00115   {
00116     precondition(input1.size() == input2.size());
00117     oln_iter_type(I1) p(input1);
00118     for_all(p) f(input1[p], input2[p]);
00119     return f;
00120   }

const window3d& win_c18_only (   )  [inline]
 

Create a window (3 dimensions) of 18 elements.

Returns:
The new window.

Definition at line 214 of file window3d.hh.

References coord. 

00215   {
00216     static const coord crd[] = { -1, -1,  0,
00217                                  -1,  0, -1,
00218                                  -1,  0,  0,
00219                                  -1,  0,  1,
00220                                  -1,  1,  0,
00221                                  0, -1, -1,
00222                                  0, -1,  0,
00223                                  0, -1,  1,
00224                                  0,  0, -1,
00225                                  0,  0,  1,
00226                                  0,  1, -1,
00227                                  0,  1,  0,
00228                                  0,  1,  1,
00229                                  1, -1,  0,
00230                                  1,  0, -1,
00231                                  1,  0,  0,
00232                                  1,  0,  1,
00233                                  1,  1,  0 };
00234     static window3d win(18, crd);
00235     return win;
00236   }

const window3d& win_c18p (   )  [inline]
 

Create a window (3 dimensions) of 19 elements.

Returns:
The new window.
It's the same than win_c18_only() plus the 0,0,0 point.

Definition at line 245 of file window3d.hh.

References coord. 

00246   {
00247     static const coord crd[] = { -1, -1,  0,
00248                                  -1,  0, -1,
00249                                  -1,  0,  0,
00250                                  -1,  0,  1,
00251                                  -1,  1,  0,
00252                                  0, -1, -1,
00253                                  0, -1,  0,
00254                                  0, -1,  1,
00255                                  0,  0, -1,
00256                                  0,  0,  0,
00257                                  0,  0,  1,
00258                                  0,  1, -1,
00259                                  0,  1,  0,
00260                                  0,  1,  1,
00261                                  1, -1,  0,
00262                                  1,  0, -1,
00263                                  1,  0,  0,
00264                                  1,  0,  1,
00265                                  1,  1,  0 };
00266     static window3d win(19, crd);
00267     return win;
00268   }

const window3d& win_c26_only (   )  [inline]
 

Create a window (3 dimensions) of 26 elements.

Returns:
The new window.

Definition at line 275 of file window3d.hh.

References coord. 

00276   {
00277     static const coord crd[] = { -1, -1, -1,
00278                                  -1, -1,  0,
00279                                  -1, -1,  1,
00280                                  -1,  0, -1,
00281                                  -1,  0,  0,
00282                                  -1,  0,  1,
00283                                  -1,  1, -1,
00284                                  -1,  1,  0,
00285                                  -1,  1,  1,
00286                                  0, -1, -1,
00287                                  0, -1,  0,
00288                                  0, -1,  1,
00289                                  0,  0, -1,
00290                                  0,  0,  1,
00291                                  0,  1, -1,
00292                                  0,  1,  0,
00293                                  0,  1,  1,
00294                                  1, -1, -1,
00295                                  1, -1,  0,
00296                                  1, -1,  1,
00297                                  1,  0, -1,
00298                                  1,  0,  0,
00299                                  1,  0,  1,
00300                                  1,  1, -1,
00301                                  1,  1,  0,
00302                                  1,  1,  1 };
00303     static window3d win(26, crd);
00304     return win;
00305   }

const window3d& win_c26p (   )  [inline]
 

Create a window (3 dimensions) of 27 elements.

Returns:
The new window.
It's the same than win_c26_only() plus the 0,0,0 point.

Definition at line 314 of file window3d.hh.

References coord. 

00315   {
00316     static const coord crd[] = { -1, -1, -1,
00317                                  -1, -1,  0,
00318                                  -1, -1,  1,
00319                                  -1,  0, -1,
00320                                  -1,  0,  0,
00321                                  -1,  0,  1,
00322                                  -1,  1, -1,
00323                                  -1,  1,  0,
00324                                  -1,  1,  1,
00325                                  0, -1, -1,
00326                                  0, -1,  0,
00327                                  0, -1,  1,
00328                                  0,  0, -1,
00329                                  0,  0,  0,
00330                                  0,  0,  1,
00331                                  0,  1, -1,
00332                                  0,  1,  0,
00333                                  0,  1,  1,
00334                                  1, -1, -1,
00335                                  1, -1,  0,
00336                                  1, -1,  1,
00337                                  1,  0, -1,
00338                                  1,  0,  0,
00339                                  1,  0,  1,
00340                                  1,  1, -1,
00341                                  1,  1,  0,
00342                                  1,  1,  1 };
00343     static window3d win(27, crd);
00344     return win;
00345   }

const window1d& win_c2_only (   )  [inline]
 

Create a window (1 dimension) of 2 elements (-1, 1).

Returns:
The new neighborhood.

Definition at line 175 of file window1d.hh.

References coord. 

00176   {
00177     static const coord crd[] = { -1, 1 };
00178     static const window1d win(2, crd);
00179     return win;
00180   }

const window1d& win_c2p (   )  [inline]
 

Create a window (1 dimension) of 3 elements (-1, 0, 1).

Returns:
The new neighborhood.

Definition at line 187 of file window1d.hh.

References coord. 

00188   {
00189     static const coord crd[] = { -1, 0, 1 };
00190     static const window1d win(3, crd);
00191     return win;
00192   }

const window2d& win_c4_only (   )  [inline]
 

Create a window (2 dimensions) of 4 elements.

Returns:
The new window.

Definition at line 186 of file window2d.hh.

References coord. 

00187   {
00188     static const coord crd[] = { -1,0,  0,-1, 0,1,  1,0 };
00189     static const window2d win(4, crd);
00190     return win;
00191   }

const window2d& win_c4p (   )  [inline]
 

Create a window (2 dimensions) of 5 elements.

Returns:
The new window.
It's the same than win_c4_only() plus the 0,0 point.

Definition at line 200 of file window2d.hh.

References coord. 

00201   {
00202     static const coord crd[] = { -1,0,  0,-1, 0,0, 0,1,  1,0 };
00203     static const window2d win(5, crd);
00204     return win;
00205   }

const window3d& win_c6_only (   )  [inline]
 

Create a window (3 dimensions) of 6 elements.

Returns:
The new window.

Definition at line 177 of file window3d.hh.

References coord. 

00178   {
00179     static const coord crd[] = { -1,  0,  0,
00180                                  0, -1,  0,
00181                                  0,  0, -1,
00182                                  0,  0,  1,
00183                                  0,  1,  0,
00184                                  1,  0,  0};
00185     static const window3d win(6, crd);
00186     return win;
00187   }

const window3d& win_c6p (   )  [inline]
 

Create a window (3 dimensions) of 7 elements.

Returns:
The new window.
It's the same than win_c6_only() plus the 0,0,0 point.

Definition at line 196 of file window3d.hh.

References coord. 

00197   {
00198     static const coord crd[] = { -1,  0,  0,
00199                                  0, -1,  0,
00200                                  0,  0, -1,
00201                                  0,  0,  0,
00202                                  0,  0,  1,
00203                                  0,  1,  0,
00204                                  1,  0,  0};
00205     static const window3d win(7, crd);
00206     return win;
00207   }

const window2d& win_c8_only (   )  [inline]
 

Create a window (2 dimensions) of 8 elements.

Returns:
The new window.

Definition at line 212 of file window2d.hh.

References coord. 

00213   {
00214     static const coord crd[] = { -1,-1, -1,0, -1,1,  0,-1, 0,1,  1,-1,  1,0,  1,1 };
00215     static const window2d win(8, crd);
00216     return win;
00217   }

const window2d& win_c8p (   )  [inline]
 

Create a window (2 dimensions) of 9 elements.

Returns:
The new window.
It's the same than win_c8_only more the 0,0 point.

Definition at line 226 of file window2d.hh.

References coord. 

00227   {
00228     static const coord crd[] = { -1,-1, -1,0, -1,1,  0,-1, 0,0, 0,1,  1,-1,  1,0,  1,1 };
00229     static const window2d win(9, crd);
00230     return win;
00231   }

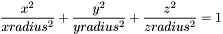
Generated on Thu Apr 15 20:13:53 2004 for Olena by doxygen 1.3.6-20040222